"Círculos y Ejes radicales"

(Un tópico de la Geometría del Círculo)

Resumen

El presente  material contiene actividades para ser realizadas con el software Cabri-géomètre (Software de la Texas Instruments), conducentes a introducir  el tema de ejes radicales. Las actividades propuestas  fueron diseñadas para ser usadas con profesores y eventualmente estudiantes, que tengan conocimientos básicos de geometría.
El objetivo es presentar el concepto de eje radical entre dos circunferencias. Este concepto generaliza el  de mediatriz de un segmento. (Mediatriz: Recta perpendicular por el punto medio a un segmento).

Agradecimientos

Los autores agradecen a los profesores Claudio DEL PINO y Juanita ?, profesores de la Universidad de Talca en la ciudad de Talca (Chile) por la organización e invitación a participar en el  evento "..", para el cual se preparó estas notas. También a la compañía Texas Instruments por su colaboración en la realización de dicho evento.

Introducción

Consideremos  los siguientes problemas:

Problema 1.

Dada una circunferencia y un punto exterior, trazar una segunda circunferencia con centro en el punto dado y que sea ortogonal a la primera.

Problema 2.

Dadas dos circunferencias exteriores trazar una tercera circunferencia ortogonal a las dos dadas.

Problema 3.

Dadas tres circunferencias exteriores sin puntos comunes cuelesquiera trazar una cuarta circunferencia ortogonal a las tres dadas.

La solución a los problemas anteriores, los cuales pudieron haberse planteado de una forma más general, sin la exigencia que fuesen exteriores  o que tuviesen puntos comunes, se mostrará en el desarrollo de estas notas. Dicha solución  geométrica involucra el concepto de ejes radicales, y éste a s vez el de potencia.
La razón fundamental de haber colocado a los problemas las condiciones restrictivas mencionadas es que "la potencia de un punto respecto a una circunferencia dada la definiremos como  el cuadrado de la medida de los segmentos tangentes trazados desde el punto a la circunferencia".

Tangentes

Segmentos Tangentes a una circunferencia desde un punto exterior.

Objetivo: Dada una circuferencia y un punto exterior trazar los segmentos tangentes a la circunferencia desde el punto. (Definición:El cuadrado de la medida de dichos segmentos se llama la potencia del punto respecto de la circunferencia.)

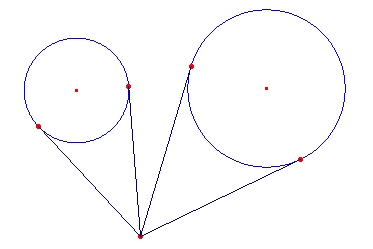
Actividad 1. Trazar los segmentos tangentes a una circunferencia desde un punto exterior.

  1. Trace un circunferenica con centro O.
  2. Trace un punto exterior P a la circunferencia.
  3. Trace el segmento OP.
  4. Halle el punto medio M del segmento OP.
  5. Trace una circunferencia con centro  en M y que pase por P.
  6. Determine los puntos A y B interceptos de las dos circunferencias.
  7. Trace los segmentos PA y PB.
  8. Oculte el semento OP, la circunferencia con centro M y el punto M.
  9. Mueva el punto P, observe y concluya.
  10. Porqué esta construcción geométricamente es correcta?

Ver archivo en Cabri: tan1.fig

Actividad 2. Realizar la Macro-Construcción.

  1. Escoja como Objetos Iniciales: La circunferencia y el punto P.
  2. Escoja como Objetos Finales: Los segmentos PA y PB.
  3. Escoja la opción: Definir la Macro. En Nombre de la construcción escriba: tangentes. En Nombre del primer objeto final, escriba: segmento tangente. En Ayuda para esta macro escriba: Seleccione una circunferencia y un punto exterior para trazar los segmentos tangentes a la circunferencia desde el punto.
  4. Seleccione la opción Guardar archivo y dé un Clic en OK.

Actividad 3. Comprobación de la Macro

  1. Dibuje dos circunferencias con centros diferentes y radios diferentes.
  2. Trace un punto P exterior a ambas circunferencias.
  3. Use la macro "tangentes" para trazar los segmentos tangentes a una y otra circunferencia.
  4. Mida estos cuatro segmentos.
  5. Mueva el punto P.
  6. Cambie de posición las circunferencias.
  7. Trace el segmento que une los centros de las circunferencias.
  8. Trace la mediatriz del segmento anterior.
  9. Reduzca el radio de una circunferencia a cero (el mínimo posible).
  10. Qué puede decir al respecto?.
  11. Reduzca el otro radio de la segunda circunferencia.
  12. Qué observa?

Ver archivo en Cabri: tan2.fig

Actividad 4. Solución al problema 1.

Emplee lo aprendido hasta el momento para resolver  el  Problema 1. Discuta su solución.

Potencia

Objetivo: Conjeturar, a partir de la potencia, cuál debe ser el lugar geométrico de los puntos que tienen igual potencia respecto a dos circunferencias dadas.

Definición: Dada una circunferencia y un punto exterior, la potencia del punto respecto a la circunferencia se define como el cuadrado de la distancia desde el punto hasta los puntos de tangencia sobre las tangentes trazadas desde el punto.

Nota: El concepto de potencia puede generalizarse para puntos interiores a la circunferencia pero no lo haremos en estas notas.

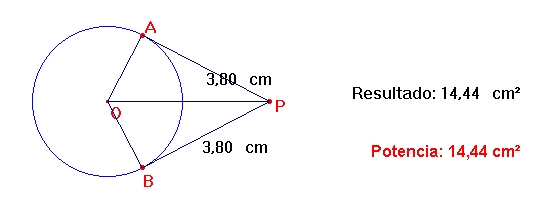
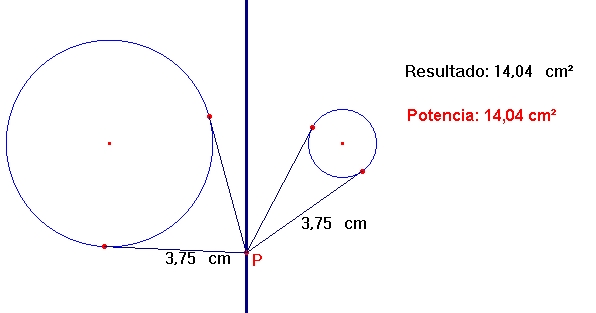
Actividad. Calcular la potencia de un punto respecto a una circunferencia.

  1. Construya una circunferencia con centro O y radio arbitrario.
  2. Trace un punto exterior P.
  3. Use la macro "Tangentes"  para trazar las tangentes desde P hasta la circunferencia.
  4. Llame los puntos de tangencia A y B.
  5. Mida cada una de los segmentos tangentes trazados PA y PB .
  6. Use la calculadora para calcular la potencia de P respecto a la circunferencia.
  7. Mueva P.
  8. Trace los segmentos OP, OA y OB.
  9. Cómo son los triángulos POA y POB?
  10. Compruebe que la potencia también se puede calcular con la distancia del punto P al centro O y el radio de la circunferencia. (Use Teorema de Pitágoras).
  11. Mueva P de tal forma que la potencia sea:
    1. 25
    2. 10
    3. 5
    4. 1
    5. 0.05
  12. Mueva P de tal manera que la potencia permanezca "constante" (cualquier número aproximado entre 20 y 25).
  13. Cuál es el lugar geométrico de tales puntos? Porqué?

Ver archivo en Cabri: pot1.fig

Eje Radical

Objetivo: Dadas dos circunferencias  construir geométricamente el eje radical.

Definición. Dados dos circunferencias cualquiera, el eje radical de las dos circunferencias se define como el lugar geométrico de todos los puntos que tienen igual potencia respecto a las circunferencias.

Actividad 1. Dónde se encuentra  aproximadamente el eje radical?

  1. Trace dos circunferencias exteriores con centros O y O' respectivamente y radios diferentes arbitrarios.
  2. Dibuje un punto P exterior a las dos circunferencias.
  3. Trace el segmento OO'. Este segmento pertenece a una recta que llamaremos "línea de los centros".
  4. Halle el punto medio de OO' y llámelo M.
  5. Trace la mediatriz de OO' por M.
  6. Use la macro "tangentes"  para trazar los segmentos tangentes desde P a cada una de las circunferencias.
  7. Use la calculadora y calcule las potencias desde el punto P a cada una de las circunferencias.
  8. Coloque estos dos números  cerca el uno del otro de tal manera que usted los pueda ver cuando mueve P.

Ver imagen en Cabri: pot2.fig

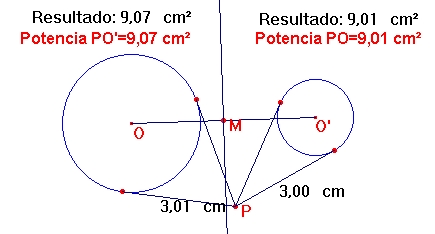
  1. Mueva P y verifique que sus potencias cambian.
  2. Mueva P de tal manera que aunque las potencias cambien las potencias respectivas sean "aproximadamente"  iguales.
  3. El punto P, con la condición anterior, describe un lugar geométrico llamado el eje radical. Aunque el lugar geométrico no lo observa en pantalla responda las siguientes preguntas:
    1. Cómo es aproximadamente este lugar?
    2. Dónde se encuentra apoximadamente?
    3. Comparando su posición relativa con la mediatriz del segmento OO' dónde se encuentra?.
    4. M pertenece al eje radical?
    5. El eje radical intercepta la línea de los centros?
    6. En caso afirmativo marque una buena aproximación  de este punto y llámelo I.
    7. Cómo son el eje radical y la línea de los centros?
    8. Cómo son el eje radical y la mediatriz de OO'?
    9. En qué posición relativa se encuentra I respecto a O y O'? (Describa su respuesta en término de los radios de las circunferencias).
  4. Modifique los radios de las circunferencias y conteste la pregunta anterior para el caso cuando:
    1. ambos radios  son iguales,
    2. uno de los dos es cero,
    3. ambos son cero,
  5. Qué puede concluir?

Actividad 2. Construcción del eje radical.

  1. Trace dos circunferencias exteriores sin puntos comunes con centros O y O'  y radios arbitrarios R y r respectivamente, donde R > r.
  2. Trace la línea  de los centros y el segmento OO'.
  3. Halle el punto medio de OO' y llámalo M.
  4. Halle las intercepciones de la circunferencia con centro en O y radio R (radio mayor) y la línea de los centros.
  5. Llame Z al intercepto más cercano  de M.
  6. Por O' trace una perpendicular al eje de los centros.
  7. Llame A', B' a los interceptos de la perpendicular anterior con la circunferencia de radio r.
  8. Por A' trace una paralela a la línea de los centros.
  9. Por Z trace una perpendicular a la línea  de los centros.
  10. Llame Z' a la intercección de las dos últimas rectas trazadas. (Vea figura adjunta)
  11. Trace una circunferencia de centro Z y radio |ZZ'|.
  12. Llame Q al punto de intersección más cercano de O de esta circunferencia con la línea de los centros.
  13. Trace una circunferencia de centro O y que pase por Q.
  14. Use la macro "tangentes"  para trazar los segmentos tangentes desde O' a la circunferencia con centro O y que pasa por Q (radio R-r).
  15. Llame los puntos de tangencia A y B respectivamente.
  16. Trace los segmentos OA y OB.
  17. Trace una paralela por O' al segmento OA y llame S la intersección de esta recta con la circunferencia de centro O'.
  18. Trace una perpendicular por S a la reta O'S.
  19. Llame T al intercepto de esta última recta con la recta que pasa por O y A. (es un punto tangente)
  20. Determine el segmento ST.
  21. Halle el punto medio J del segmento ST.
  22. Trace una perpendicular por J a la línea de los centros. La recta obtenida es el eje radical.

Observación: El último paso de trazar una perpendicular a la línea de los centros por J, es por el hecho que la construcción de un segundo punto J' relacionado con el punto B es una construccción simetrica respecto a la línea de los centros.

Ver figura en Cabi: rad1.fig

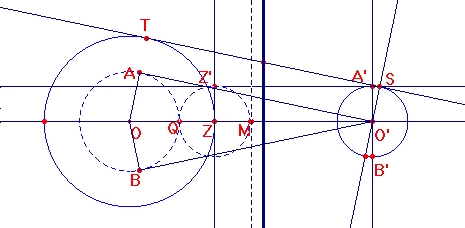
  1. Mueva O y O'.  Qué observa?
  2. Modifique los radios de las circunferencias. Qué observa?.
  3. Tome un punto sobre el eje radical y con la macro "Tangentes"  trace los segmentos tangentes.
  4. Cual es la potencia de ese punto respecto a cada una de las circunferencias?.
  5. Cómo puede argumentar geométricamente que la construcción anterior es correcta y por tanto afirmar que efectivamerte el eje encontrado es el eje radical?. Discuta con sus compañeros esta construcción.

Actividad 3. Crear una macro para construir el eje radical.

  1. No borre la figura anterior.
  2. Construya la macro macro macro "Eje Radical" con objetos iniciales las dos circunferencias y objetos finales el eje radical.
  3. Abra una plantilla nueva y verifique su macro.

Actividad 4. Solución al problema 2.

Dadas dos circunferencias construir una tercera circunferencia que sea ortogonal a las dos dadas.

  1. Trace dos circunferencias exteriores sin puntos comunes.
  2. Use la macro "Eje Radical" y construya el eje radical.
  3. Tome un punto cualquiera P sobre el eje radical.
  4. Mueva P.
  5. Con la macro "Tangentes" trace los segmentos tangentes.
  6. Llame los puntos de tangencia A,B, y A',B' de la primera y segunda circunferencia respectivamente.
  7. Use la calculadora y calcule la potencia de P a ada una de las circunferencias.
  8. Con centro en P trace una tercera circunferencia que pase por A.
  9. Pasa esta circunferencia por los demás puntos de tangencia?. Por qué?
  10. Mueva P.
  11. Con qué ángulo se interceptan las tres circunferencias?
  12. Qué puede concluir respecto a la solución del problema de hallar una tercera circunferencia ortogonal a dos dadas?.
  13. De nuevo mueva P, modifique la posición de los centros y los radios de las circunferencias.

Ver figura en Cabri: rad2.fig

Actividad 4. Eje radical vs. mediatriz.

  1. Trace dos circunferencias exteriores sin puntos comunes con centros O y O'
  2. Trace el segmento OO'.
  3. Trace la mediatriz del segmento OO' (use la macro: Mediatriz: Perpendicular por el punto medio de un segmento).
  4. Trace el eje radical (use la macro).
  5. Compare la posición relativa de la mediatriz y el eje radical.
  6. Modifique la posición de los centros y los radios de las circunferencias.
  7. Mida los radios de las circunferencias.
  8. Coloque una posición tal que los radios de las circunferencias sean iguales. Conteste la pregunta 5 (subrayada)
  9. Modifique el radio de una de las circunferencias hasta obtener un radio igual a cero. Conteste la pregunta 5 (subrayada)
  10. Modifique ambos radios de las circunferencias hasta obtener radios iguales a cero. Conteste la pregunta 5 (subrayada)
  11. Qué puede concluir?

Centro Radical

Objetivo: Dadas tres circunferencias construir una cuarta circunferencia ortogonal a las tres dadas, es decir construir la solución aal problema 3.

Actividad: Construir el centro radical de tres circunferencias exteriores sin puntos comunes.

En esta actividad se va a resolver un problema de tipo "Problemas de Apolonio": Dadas tres circunferencias encontrar una cuarta circunferencia ortogonal a las tres dadas. Esta actividad es libre y se espera que con todo lo anterior se pueda resolver geométricamente y argumentar matemáticamente su construcción. No olvide discutir la posición relativa de las tres circunferencias.

Conclusiones

  1. El concepto de eje radical entre dos circunferencias generaliza el concepto de mediatriz de un segmento. Esto se puede visualizar a medida que se reducen los radios a medida cero.
  2. El centro radical, que es el punto desde el cual, tomado como centro, se traza una circunferencia ortogonal a tres circunferencias dadas, es la generalización del circuncentro de un triángulo es decir un punto equidistante a los tres vértices del triángulo. Al igual que para hablar de circuncentro se necesita que los tres vértices no sean colineales para hablar de centro radical exigimos que los centros de las circunferencias no sean colineales.